“Do I have enough filament to print this one thing?” That’s the question on my mind whenever I’m nearing the end of a reel of filament. I can’t stand wasting a few meters of filament by underestimating what’s left, and I don’t want to unwind a few meters of filament just to measure it and wind it back on the reel.

Math to the rescue! Now I simply count the number of loops of filament left on the reel, then multiply by the circumference of the reel to estimate how many meters of filament is left. Let’s break that process down:

Step 1: Measure the diameter of your filament reel’s hub. Notice in the picture above that I’m measuring the inside diameter of the hub rather than its outside diameter. I do this because it’s sometimes hard to get a good outside measure of a hub that has 15 or 20 loops of filament on it. Luckily using the inside diameter will just make my estimate more conservative: I won’t overestimate how much filament I have. My Village Plastics reel measured 89.59 mm, so I round up to 90 mm. TIP: when you have emptied a reel, measure its hub’s outside diameter and keep that measurement for your next estimate.

Step 2: Calculate the circumference of the hub.  Remember from your early math classes that C = PI * D, where C is the circumference of a circle, D is its diameter, and PI is the lovely constant that ties the two together. I use 3.14 as a rough value of PI because I don’t need an exact number. So C = 3.14 * 90 mm = 282.6 mm circumference. I round that to 282 mm, again because this is a rough, back-of-the-envelope estimate.

Step 3: Convert mm per loop of filament (hub circumference) to loops per meter: 1000 mm per meter divided by 282 mm per loop = 3.54 loops per meter.  I’ll round to 3.5 loops per meter.

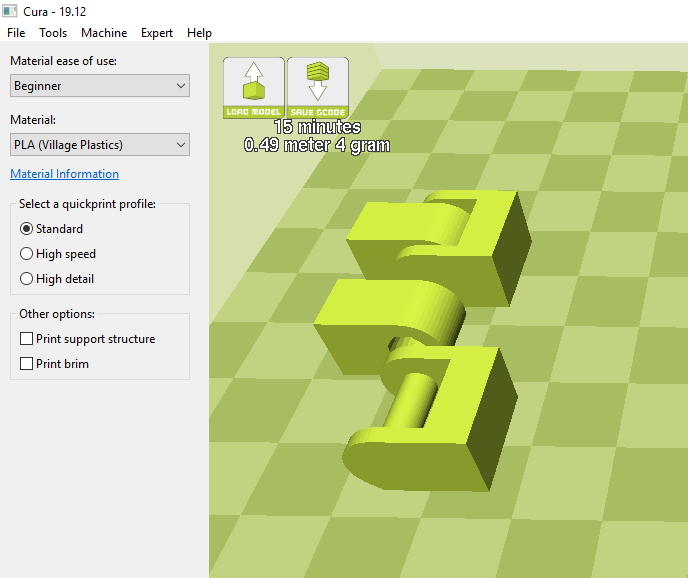
Step 4: Estimate the length of filament required for your print. Luckily Cura, the slicer software I use, estimates that number for me. For this print, Cura says it will take 0.49 meters, which I round to 0.5 meters.

Step 5: Convert that length to a number of loops required. 0.5 meter times 3.5 loops per meter = 1.75 loops.  I call that “Under 2 loops”.

Step 6: Count the number of loops of filament remaining on the reel. In the photo above I count about 3 loops, so I have more than the 2 loops required. The print is a go!

Yes, math works! As you can see, the print finished with a loop or two to spare. The remaining filament is short enough that I can directly measure its length if I want to try another print.

I’ve found this technique works nicely any time I can count the loops of filament remaining on the reel, which for my reels is about 20 loops, or over 5 meters (20 loops / 3.5 loops per meter = about 5.7 meters). So unless I’m printing something really big, I can know whether I should press Print or instead load up a fresh reel of filament.